1.      Точность импульсных систем.

 

Для импульсных систем, как и для непрерывных, введены определения статической ошибки, астатизма, коэффициентов ошибок, ошибки при гармоническом воздействии, а также средней квадратической ошибки [13].

Установившиеся ошибки. Точность работы импульсных систем в установившемся режиме оценивается по величине установившейся ошибки при различных типовых входных воздействиях, наиболее характерных для исследуемой системы.

 В замкнутой импульсной системе (рис. 1.10) ошибка x, задающее воздействие g и возмущающее воздействие f связаны, как следует из выражений (1.73) и (1.76), следующей зависимостью относительно z-изображений

 

X(z,s) = X_g(z,s) + X_f(z,s) =                       (1.105)

 

Выражение (1.105) содержит z-изображения двух составляющих ошибки: X_g(z,s) - от задающего и X_f(z,s) - от возмущающего воздействий.

Установившаяся ошибка импульсной системы определяется по предельному значению решетчатой функции (1.37):

 

(1.106)

где x_g(¥,s) - установившаяся ошибка от задающего воздействия;

       x_f(¥,s) - установившаяся ошибка от возмущающего воздействия.

В большинстве случаев ограничиваются рассмотрением ошибки в дискретные моменты времени t = nT. Однако, надо иметь в виду, что в импульсных системах могут возникать малые колебания внутри периода дискретности в установившемся режиме.

Выражение для установившейся ошибки (1.106) при s = 0 будет

 

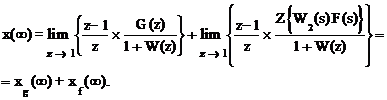   (1.107)

 

Установившиеся ошибки замкнутой импульсной системы от задающего воздействия находятся при f = 0.

При g(t) = g₀ ´1(t)  установившаяся ошибка определяется как

 

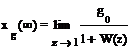
и называется статической ошибкой или ошибкой системы по положению.

При g(t) = g₁´t  установившаяся ошибка называется ошибкой системы от скорости и определяется как

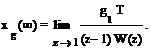
Если  , то получаем ошибку системы от ускорения

 

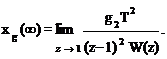
Из последних двух выражений следует, что установившаяся ошибка от задающего воздействия импульсной системы не только прямо пропорциональна величине задающего воздействия, но и периоду дискретности.

Импульсные системы классифицируются в соответствии с числом полюсов дискретной передаточной функции разомкнутой системы W(z) при z = 1. Если дискретная передаточная функция импульсной разомкнутой системы

,

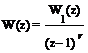а W₁(z) не содержит полюсов при z = 1, то при r = 0 система называется статической, при r = 1 - астатической первого порядка и т.д. В астатических системах W(1)® ¥.

 Для того чтобы импульсная система имела нулевую установившуюся ошибку от задающего воздействия, необходимо, чтобы степень астатизма r системы превышала степень полинома k входного воздействия, то есть

x_g(¥) = 0, если k < r ;

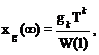 если k = r ;

x_g(¥) = ¥, если k > r .

 

Коэффициенты ошибок. Если задающее воздействие g(t) имеет произвольный вид, предельное значение ошибки вычисляется по формуле

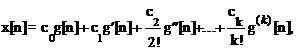         (1.108)

где  c₀, c₁, c₂, ...  - коэффициенты ошибок по положению, скорости, ускорению и т.д.

Коэффициенты ошибок находят по дискретной передаточной функции замкнутой импульсной системы по ошибке

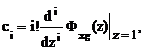 для i = 0, 1, 2, ..., k.           (1.109)

Число коэффициентов находится в соответствии с наибольшей степенью полинома входного воздействия.

В астатических системах несколько первых коэффициентов ошибок равны нулю: c₀ = c₁ = ... = c_r-1 = 0, где r - степень астатизма.

Ошибки импульсных систем при гармоническом воздействии. Задающее синусоидальное воздействие g(t) = g_msin(wt) произвольной частоты w преобразуется на входе в решетчатое гармоническое воздействие g[nT] = g_m sin[wnT].

При этом установившаяся ошибка в линейной замкнутой импульсной системе будет

 

x[nT] = x_m sin[wnT+y],                           (1.110)

 

где  x_m  = ½Ф_xg(e^jwT)½´g_m ,  y(w,s) = arg Ф_xg(e^jwT).

Как установлено в разделе 1.6, в полосе пропускания системы частотные характеристики импульсной системы практически совпадают с частотными характеристиками ее непрерывной части, поэтому для определения ошибки импульсной системы при гармоническом воздействии можно пользоваться методикой для непрерывных систем.

Статистическая точность импульсных систем исследуется аналогично непрерывным системам. При прохождении случайного сигнала через импульсную систему ее выходная координата и ошибка воспроизведения представляют собой тоже случайные процессы.

Качество работы импульсной системы при стационарных случайных воздействиях оценивается средними значениями квадрата выходной переменной

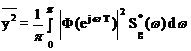                    (1.111)

и квадрата ошибки

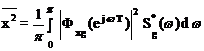 ,                 (1.112)

где  Ф(e^jwT) и Ф_xg(e^jwT) - частотные передаточные функции замкнутой импульсной системы;

       - спектральная плотность решетчатого случайного процесса на входе системы.