1.      Интегрирующие и дифференцирующие динамические звенья и их характеристики?

 

Интегрирующие звенья

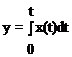В звеньях интегрирующего типа линейной зависимостью  связаны в установившемся режиме производная выходной величины и входная величина. В этом случае для установившегося режима будет справедливым равенство , откуда и произошло название этого типа звеньев.

Идеальное интегрирующее звено. Уравнение и передаточная функция имеют вид

py(t) = x(t),    .                              (3.28)

Амплитудно-фазовая частотная характеристика:

W(jw) = ,    A(w) = ,   y(w) = -900.                (3.29)

Переходная и импульсная функции:

 

h(t) = t,     w(t) = 1(t).                                (3.30)

 

Такое звено является идеализацией реальных интегрирующих звеньев.

Примерами идеальных интегрирующих звеньев могут служить операционный усилитель в режиме интегрирования, гидравлический двигатель, емкость и др.

 

Дифференцирующие звенья

 

В звеньях дифференцирующего типа линейной зависимостью   связаны в установившемся режиме выходная величина и производная входной, откуда и произошло название этого типа звеньев.

Идеальное дифференцирующее звено. Уравнение и передаточная функция имеют вид

y(t) = px(t),   W(s) = s .                               (3.31)

 

Амплитудно-фазовая частотная характеристика:

 

W(jw) = jw,  A(w) = w,  y(w) = +900.                (3.32)

 

Переходная и импульсная функции:

h(t) = d(t),     w(t) =  .                          (3.33)

Такое звено является идеализацией реальных дифференцирующих звеньев.

Примерами идеальных дифференцирующих звеньев могут служить операционный усилитель в режиме дифференцирования, тахогенератор и др.

Форсирующее (дифференцирующее) звено первого порядка. Дифференциальное уравнение и передаточная функция

 

 y(t) = (tp+1) x(t) ,  W(s) = ts+1,                     (3.34)

 

где t - постоянная времени дифференцирования.

Амплитудно-фазовая частотная характеристика:

W(jw) = (jwt + 1),   A(w)=,   y(w) =  arctg wt .    (3.35)

 

Переходная и импульсная функции:

h(t) = 1(t) + td(t),     w(t) = d(t) + t .                     (3.36)

Форсирующее (дифференцирующее) звено второго порядка. Уравнение и передаточная функция звена:

 

y(t) = (t2p2+2xtp+1)x(t),  W(s) = t2s2+2xts+1.               (3.37)

 

Амплитудно-фазовая частотная характеристика:

 

W(jw) = (1-w2t2) + j2xwt, 

 

A(w)=,    y(w)=arctg.  (3.38)

Переходная и импульсная функции:

h(t) = t2+2xtd(t)+1(t),     w(t) = t2+2xt+d(t).    (3.39)