1.      Критерий устойчивости Гурвица?

 

Линейная система, характеристический полином которой равен

,

где a0>0, устойчива, если положительны n главных определителей матрицы Гурвица:

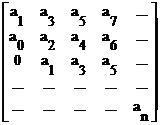                            (5.8)

 

Порядок составления матрицы Гурвица следующий. На главной диагонали записываются все коэффициенты,  начиная с первого. Далее заполняются строки: четными коэффициентами по порядку, если на главной диагонали стоит четный коэффициент, и нечетными, если на главной диагонали стоит нечетный коэффициент. Если какой-либо коэффициент отсутствует, то вместо него заносится нуль.

Для оценки устойчивости системы необходимо вычислить определители Гурвица Di (i = 1, 2, ... , n), которые получают из матрицы (5.8) путем отчеркивания равного числа строк и столбцов в левом верхнем углу матрицы.

Система устойчива, если Di > 0   для всех i = 1, 2, ... , n.

Последний определитель Гурвица, как видно из приведенной выше матрицы, равен

Dn = an ´ Dn-1.

Поэтому его положительность сводится при Dn-1>0 к условию an>0,

Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов ai.

Если определитель Dn=0, то система находится на границе устойчивости. Возможны два случая: апериодическая граница устойчивости, если свободный член характеристического уравнения равен нулю, что соответствует нейтрально устойчивой системе;  колебательная граница устойчивости,  если определитель    Dn-1=0. Из условия Dn-1=0 можно определить параметры, при которых система находится на границе устойчивости.