1.      Оценка качества управления при периодических задающих воздействиях.

 

Рассмотрим теперь установившееся состояние при изменении задающего воздействия с постоянной скорость g(t)=g1´t (где g1=const) и постоянном значении возмущающего воздействия f(t)=f0=const. По (6.4) найдем установившуюся ошибку:

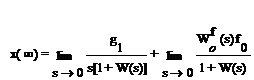                  (6.10)

 

Первый член этого выражения в статической системе при W(0)=k стремится к бесконечности, поэтому система, работающая в режиме слежения с постоянной скоростью, должна быть астатической относительно задающего воздействия. Второе слагаемое определяет статическую ошибку системы от возмущающего воздействия.

Для систем с астатизмом первого порядка установившаяся ошибка от задающего воздействия

= g1/kv,                                       (6.11)

 

где kv - коэффициент передачи (добротность) системы по скорости.

Ошибка  называется скоростной ошибкой от задающего воздействия.

В системах с астатизмом второго порядка и выше скоростная ошибка равна нулю (так как kv®¥), поэтому режим с задающим воздействием, изменяющимся с постоянной скоростью, используется только для оценки точности следящих систем с астатизмом первого порядка.

Рассмотрим установившийся режим в системе при изменении задающего воздействия с постоянным ускорением g(t)=g2´t2/2 (где g2=const) и постоянным значением возмущающего воздействия f(t)=f0=const.

Аналогично определяется установившаяся ошибка по (6.4):

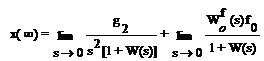                (6.12)

В статических и астатических системах первого порядка первая составляющая ошибки стремится к бесконечности, поэтому этот режим имеет смысл только для следящих систем с астатизмом второго порядка, для которых ошибка по задающему воздействию

= g2/ka,                                     (6.13)

 

где ka - коэффициент передачи (добротность) системы по ускорению.

Ошибка  называется установившейся ошибкой системы от ускорения. Этот режим работы обычно применяется для оценки точности следящих систем с астатизмом второго порядка.

Второе слагаемое, как и в предыдущем случае, определяет статическую ошибку системы от возмущающего воздействия.