1.      Примеры основных свойств обратных связей при охвате различных типов звеньев.

 

Проиллюстрируем на примерах основные свойства обратных связей WОС(s) при охвате ими различных типов звеньев WОХВ(s) (рис.8.5).

Рис. 8.5. Структурная схема обратной связи

 

Жесткая обратная связь WОС(s) = kОС.

1. Охватывает безынерционное звено WОХВ(s)=k.

Тогда эквивалентная передаточная функция будет

,

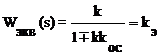где kЭ  - эквивалентный коэффициент передачи.

При ООС kЭ<k  ; при ПОС kЭ>k.

Если при ПОС kkОС=1, то kЭ®¥ , такой элемент представляет собой реле.

Следовательно, положительная обратная связь может служить для увеличения коэффициента передачи.

2.   Охватывает апериодическое звено первого порядка

.

Тогда эквивалентная передаточная функция будет

,

где  kЭ  -  эквивалентный коэффициент передачи;

       TЭ  -  эквивалентная постоянная времени.

При ООС      и     .      

Следовательно, отрицательная жесткая обратная связь уменьшает инерционность звена. Тем самым она оказывает стабилизирующее действие и улучшает качество переходного процесса в системе. Уменьшение же коэффициента передачи может быть скомпенсировано за счет других  звеньев системы.

При ПОС 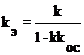     и   .

Следовательно, положительная жесткая обратная связь может служить для увеличения коэффициента передачи. Но одновременно с этим увеличивается и постоянная времени, т.е. инерционность звена, а при kkОС>1 звено становится неустойчивым.

3. Охватывает интегрирующее звено .

Тогда эквивалентная передаточная функция будет

,

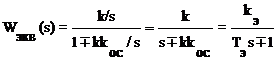где  kЭ  -  эквивалентный коэффициент передачи;

       TЭ  -  эквивалентная постоянная времени.

При ООС 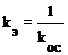        и   .

Следовательно, под действием отрицательной жесткой обратной связи интегрирующее звено превращается в апериодическое с коэффициентом передачи целиком определяемым обратной связью. Такую связь необходимо использовать в тех случаях, когда требуется понизить степень астатизма, т.е. исключить в системе влияние интегрирующего звена. При ПОС звено теряет устойчивость.

Инерционная жесткая обратная связь WОС(s) = .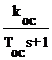

При охвате ею безынерционного звена  WОХВ(s)=k  получаем

,

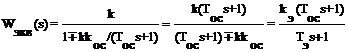где  kЭ  -  эквивалентный коэффициент передачи;

       TЭ  -  эквивалентная постоянная времени.

При ООС      и   .

Следовательно, в этом случае безынерционное звено превращается в интегро-дифференцирующее звено. Инерционное запаздывание в обратной связи (в отличие от такового в прямой цепи) целесообразно использовать для улучшения качества переходных процессов, получая эффект, аналогичный введению производной в прямой цепи. Отсюда вытекает и хорошее влияние инерционной жесткой обратной связи на качество переходного процесса в системе в целом.

Положительная инерционная жесткая обратная связь обычно не используется.

Гибкая обратная связь WОС(s) = kОС s.

При охвате ею апериодического звена первого порядка   получаем

,

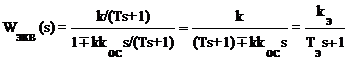где  kЭ  -  эквивалентный коэффициент передачи;

       TЭ  -  эквивалентная постоянная времени.

При ООС  kЭ=k  и  TЭ=T+kkОС, если ПОС, то kЭ=k иTЭ=T-kkОС.

Таким образом, гибкая обратная связь изменяет только инерционность звена, причем для ООС эквивалентная постоянная времени увеличивается.

Инерционная гибкая обратная связь WОС(s) = .

При охвате ею интегрирующего звена   получаем

,

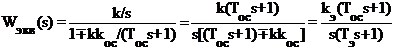где  kЭ  -  эквивалентный коэффициент передачи;

       TЭ  -  эквивалентная постоянная времени.

При ООС   и  ,

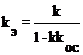при ПОС   и   .

Следовательно, охват интегрирующего звена инерционной гибкой обратной связью эквивалентен последовательному включению интегро-дифференцирующего звена. При отрицательной инерционной гибкой обратной связи и большом коэффициенте передачи k интегрирующее звено приближенно становится изодромным.

Способ коррекции местной обратной связью позволяет наилучшим образом скорректировать динамические свойства системы по сравнению со способами коррекции с помощью последовательных и параллельных корректирующих устройств.

Динамические свойства линейных систем при введении корректирующих устройств различного вида могут быть сделаны одинаковыми. Следовательно, включение любого типа корректирующего устройства может обеспечить требуемое качество работы системы. В этом случае передаточные функции регуляторов с последовательной коррекцией (8.5), параллельной коррекцией (8.6) и местной обратной связью (8.7) должны быть одинаковыми, т.е.

 

WR1(s) = WR2(s) = WR3(s).                              (8.8)

 

Отсюда следует формула перехода от передаточной функции корректирующего устройства одного вида к передаточной функции эквивалентного корректирующего устройства другого вида

W2(s)WПКУ(s) = W2(s)+WêêКУ(s) = 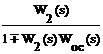.           (8.9)

Использование того или иного вида корректирующих устройств, т.е. последовательных звеньев, параллельных звеньев или обратных связей, определяется удобством технической реализации.