1.      Решетчатые функции и разностные уравнения (определения, понятие конечных разностей).

 

Решетчатая функция времени x[nT], или в сокращенной записи x[n] - это математическая функция, значения которой определены в дискретные равноотстоящие друг от друга моменты времени t = nT, где n - целое положительное число 0, 1, 2 ..., а Т - период дискретности. То есть решетчатая функция представляет собой числовую последовательность:

 

x[0], x[1T], x[2T], x[3T], ... , x[kT], ... .

 

Если период дискретности T задан, то решетчатая функция однозначно формируется из исходной непрерывной. Операция замены непрерывной функции решетчатой

                                                           (1.2)

показана на рис. 1.3.

Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками t = nT, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.

Возникает вопрос, при каких условиях возможно точное восстановление квантованной функции. Ответ на него дает теорема Котельникова-Шеннона [5]: непрерывный сигнал x(t), частотный спектр которого ограничен полосой 0 < f < f_п, полностью определяется последовательностью своих дискретных значений, если период повторения Т этих значений удовлетворяет условию

Т <     или     Т <  ,                          (1.3)

где f_п[Гц], w_п [с^-1] - частота пропускания.

 

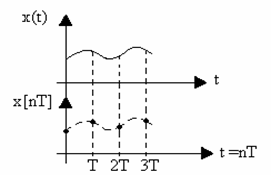
Рис. 1.3.Временные диаграммы изменения непрерывной функции x(t)

 и решетчатой функции  x[nT]

 

Разностные уравнения (уравнения в конечных разностях) связывают между собой решетчатые функции и их конечные разности. При использовании прямых разностей неоднородные линейные разностные уравнения m-го порядка имеют вид [2]

 

b₀D^my[n,s] + b₁D^m-1y[n,s] + ... + b_m-1Dy[n,s] +b_my[n,s] = f[n,s],  (1.16)

 

где f[n,s] - заданная, а y[n,s] - искомая решетчатые функции. При f[n,s] º 0 уравнение (1.16) становится однородным разностным уравнением, решением которого будет y[n,s].

При использовании (1.9) разностное уравнение (1.16) можно записать в другом виде:

 

a₀y[n+m,s] + a₁y[n+m-1,s] + ... + a_my[n,s] = f[n,s].          (1.17)

 

Коэффициенты этого уравнения определяются

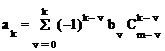,                             (1.18)

где биноминальные коэффициенты (число сочетаний)

.                                  (1.19)

При использовании обратных разностей неоднородные линейные разностные уравнения m-го порядка будут

 

b₀Ñ^my[n,s] + b₁Ñ^m-1y[n,s] + ... + b_m-1Ñy[n,s] +b_my[n,s] = f[n,s]. (1.20)

 

С учетом (1.10) последнее выражение приобретает вид

 

a₀y[n,s] + a₁y[n-1,s] + ... + a_my[n-m,s] = f[n,s].          (1.21)

 

Коэффициенты этого уравнения определяются

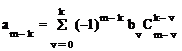,                            (1.22)

где биноминальные коэффициенты (число сочетаний)

.                                (1.23)

Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения y[n+m,s]  при n = 0, 1, 2, ... для уравнения (1.17) и заданных начальных значений y[0,s], y[1,s], ..., y[m-1,s] или значения y[n,s] при n = 0, 1, 2, ... для уравнения (1.21) и  заданных начальных значений    y[n-m,s],  y[n-m+1,s],  ..., y[n-1,s].

Решение уравнения (1.21) при s = 0 представляет собой рекуррентную формулу:

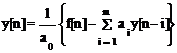,    для n=0, 1, 2, ...               (1.24)

при нулевых начальных условиях y[n] º 0 при n < 0. Структурная схема решения приведена на рис. 1.4.

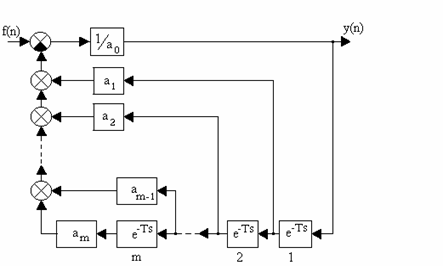                                                         Рис. 1.4.Структурная схема решения разностного уравнения

 

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

y[n,s] =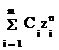,                                    (1.25)

где z_i  - корни характеристического уравнения

 

a₀ z^m + a₁z^m-1 + ... + a_m = 0,                           (1.26)

C_i - постоянные коэффициенты.

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, w-преобразование, а также частотные методы.