1.      Свойства z-преобразования.

 

 

1. Свойство линейности. Если F₁(z,s)=Z_s {f₁(t)} и F₂(z,s)=Z_s {f₂(t)}, то

Z_s {a₁f₁(t) + a₂f₂(t)}= a₁ F₁(z,s) + a₂ F₂(z,s).              (1.31)

 

2. Теорема сдвига (смещения). Если  Z_s {f(t)} = F(z,s) и t - произвольное положительное число, тогда

 

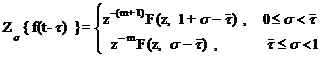        (1.32)

 

 где  ,  m - целая,   - дробная часть числа t/T;

если t = mT, тогда

Z_s {f(t-mT)}=z^-mF(z,s).                               (1.33)

 

3. Изображение обратных разностей

 

Z{Ñ^kf[nT]}= (1 - z^-1)^kF(z).                           (1.34)

 

4. Изображение конечных сумм:

полных 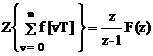         ,                            (1.35)

неполных      .                            (1.36)

 

5. Предельные значения. Если дискретные значения функции в установившемся режиме существуют, то они могут быть найдены путем следующего предельного перехода:

,                  (1.37)

начальное значение функции оригинала:

 

.                       (1.38)

 

6. Свертка функций. Если F₁(z) = Z{f₁(t)} и F₂(z) = Z{f₂(t)}, то

 

      (1.39)

и   

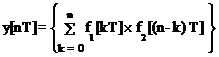                    (1.40)

 

7. Формула обращения. Дискретные значения функции по ее z-преобразованию определяют следующим контурным интегралом:

 

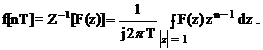           (1.41)

8. Изображение разностных уравнений. Пусть разностное уравнение, связывающее выходную координату y[nT] импульсной системы с ее входным воздействием f[nT], имеет следующий вид:

 

a₀y[n]+a₁y[n-1]+...+a_my[n-m] = b₀f[n]+b₁f[n-1]+...+b_lf[n-l],      (1.42)

при  m ³ l и y[n] º 0,  f[n] º 0 для всех n < 0.

Подвергнув исходное уравнение z-преобразованию, получим

 

a₀Y(z)+a₁ z^-1Y(z)+...+a_m z^-mY(z) = b₀F(z)+b₁ z^-1F(z)+...+b_l z^-lF(z),

 

которое можно переписать в виде

 

A(z)Y(z)=B(z)F(z),                                     (1.43)

где полиномы

 и 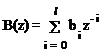   .                  (1.44)

Из (1.43) находим изображение выходной координаты

 

Y(z)=W(z)F(z),                                       (1.45)

где 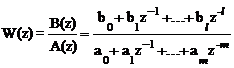                 .                     (1.46)

 

По аналогии с определением передаточной функции непрерывных систем выражение W(z) называется дискретной передаточной функцией импульсной системы.

Данная запись отличается от передаточной функции для непрерывных систем тем, что переменная z в полиномах имеет отрицательные степени. Для того, чтобы была полная аналогия с передаточными функциями непрерывных систем, степень переменной z делают положительной путем домножения числителя и знаменателя выражения (1.46) на z^m . Тогда получим формулу, которая полностью аналогична записи для непрерывной функции

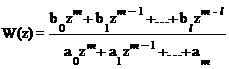.                   (1.47)