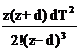1.      Связь между дискретным преобразованием Лапласа, z-преобразованием и собственно преобразованием Лапласа (с примером определения изображения по дискретному преобразованию Лапласа (z-преобразованию), соответствующего какой-либо передаточной функции непрерывной системы). Комплексный спектр решетчатой функции времени.

 

 

.               (1.28)

Функция X(z,s), определяемая выражением (1.28), называется z-преобразованием непрерывной функции времени x(t) и обозначается как

X(z,s) = Z_s {x(t)};                                     (1.29)

 

z-преобразование функции x(t) можно также представить следующим образом:

X(z,s) = Z_s {X(s)},                                     (1.30)

 

где X(s) - преобразование Лапласа от x(t). В этом случае подразумевается, что преобразованию подвергается функция времени и запись (1.30) носит чисто формальный характер.

 

Т а б л и ц а  1. 1

Z - преобразования функций времени

 

Для нахождения z-изображений решетчатых функций по заданному оригиналу и наоборот имеются специальные таблицы [2, 15,  17], фрагмент такой таблицы приведен выше. Необходимо отметить, что все функции времени, имеющие одинаковые значения в дискретные моменты времени, обладают одинаковыми z-преобразованиями и поэтому связь между функцией времени и ее z-изображением не является взаимно однозначной. Однако, семейство модифицированных z-преобразований решетчатой функции для всех s от 0 до 1 однозначно определяет непрерывную функцию.

Комплексный спектр решетчатой функции времени f[n,s] представляет собой комплексную функцию вещественного переменного w, определяемую следующим выражением:

   при  -¥ < w < ¥ .         (1.48)

 

Таким образом, для получения комплексного спектра необходимо в изображении  решетчатой функции произвести замену  z = e^jwT, откуда следует, что функция z является периодической функцией w с периодом, равным 2p/T. По этой причине комплексный спектр решетчатой функции также является периодической функцией w того же самого периода:

                     (1.49)

 

и, следовательно, может рассматриваться на любом интервале значений w, длина которого равна 2p/T. В качестве такого интервала принят интервал

                                   (1.50)

 

Подобно любой комплексной функции спектр (1.48) может быть представлен в показательной или алгебраической форме записи:

 

F(e^jwT,s) = А(w, s)´e^{jy(w, s)} = U(w, s) + jV(w, s),             (1.51)

 

где A(w, s), y(w, s), U(w, s), V(w, s) называются соответственно амплитудным, фазовым, вещественным и мнимым спектрами решетчатой функции f[n,s]. При фиксированном значении w спектр (1.51) изображается вектором в плоскости (U, jV); при изменении w от -p/T до +p/T, конец вектора F(e^jwT,s) прочерчивает некоторую кривую, которая является графическим изображением спектра.