1. Приближенный способ построения ЛЧХ
импульсных систем. Пример построения.
Для удобства логарифмические частотные характеристики
строятся отдельно для областей низких и высоких частот. Границей, разделяющей
частотную область на низкочастотную и высокочастотную,
служит частота среза wс в
предположении, что
(1.83)
где Т - период дискретности.
Последнее условие необходимо выполнять вследствие
требований, предъявляемых к обеспечению запаса устойчивости и точности работы
системы, и согласуется с теоремой Котельникова-Шеннона.
Рассмотрим методику построения ЛЧХ
на примере АИС, включающей в себя экстраполятор нулевого порядка и непрерывную
часть с передаточной функцией:
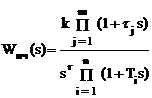. (1.84)
При построении вводят следующие предположения.
1. Величина, обратная периоду дискретности T, больше
половины частоты среза wс, т.е. wс
< 2/T.
2. Переход оси нуля децибел асимптотической ЛАХ
непрерывной части происходит при отрицательном наклоне -20 дб/дек.
3. Постоянным времени tj (j = 1, 2, ..., m) соответствуют
сопрягающие частоты меньшие, чем частота среза.
4. Имеется l (l < n) постоянных времени Ti (i = 1, 2, ..., l), которым
соответствуют сопрягающие частоты меньшие, чем частота среза.
Пример. Построить
логарифмические частотные характеристики АИС с экстраполятором нулевого порядка
и периодом дискретности импульсного элемента T = 4 с, передаточная функция непрерывной части которой
.
Р е ш е н
и е . Выбираем частоту среза wc <
2/T < 0.5 c-1. В соответствии с заданными
постоянными времени определяем сопрягающие частоты:
wcопр1=1/25=0.04
c-1 - низкочастотный диапазон;
wcопр2=1/0.5=2
c-1 - высокочастотный диапазон;
wcопр3=1/0.3=3.33
c-1 - высокочастотный диапазон.
Следовательно, получаем:
,
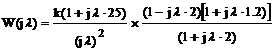где Tå = Т1+Т2=0.8;
,
lсопр1=1/25=0.04;
lсопр2=1/2=0.5;
lсопр3=1/1.2=0.8
.
Асимптотические ЛАХ и ЛФХ, соответствующие полученным выражениям,
представлены на рис. 1.12.
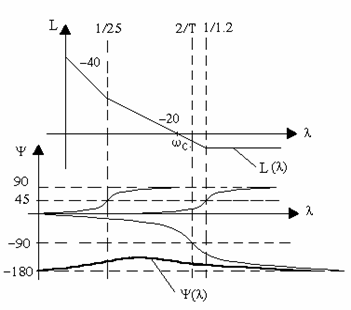
Рис. 1.12. ЛЧХ импульсной системы
