1.      Устойчивость импульсных систем.

 

Как и для непрерывных систем, устойчивость импульсных систем является необходимым условием их работоспособности.

 Устойчивость системы характеризуется ее свободным поведением, а свободное поведение определяется переходной составляющей процесса регулирования выходной величины. Линейная импульсная система называется устойчивой, если переходная составляющая процесса регулирования y_п[n,s] затухает с течением времени.

Сформулированное условие устойчивости сводится к выполнению равенства

                               (1.90)

для всех s из интервала  0 £ s < 1. Если хотя бы для одного значения s

                             (1.91)

то импульсная система называется неустойчивой. Если, наконец,

 

                          (1.92)

или не существует, то импульсная система находится на границе устойчивости.

 

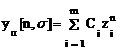,                                    (1.94)

Из решения (1.94) следует, что для устойчивости импульсной системы необходимо и достаточно, чтобы все корни характеристического полинома замкнутой системы (полюса передаточной функции замкнутой импульсной системы Ф(z, s)) удовлетворяли условию

 

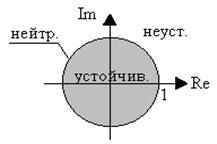
½z_i ½< 1;   i = 1, 2, ..., m.                             (1.96)

                                                                    

Если хотя бы один корень ½z_i ½> 1, система будет неустойчивой. Значением какого-либо корня ½z_i ½= 1 при всех остальных½z_i ½< 1 определяется граница устойчивости импульсной системы.

Графически область устойчивости импульсной системы на плоскости z корней характеристического уравнения изображается единичным кругом (рис. 1.13).